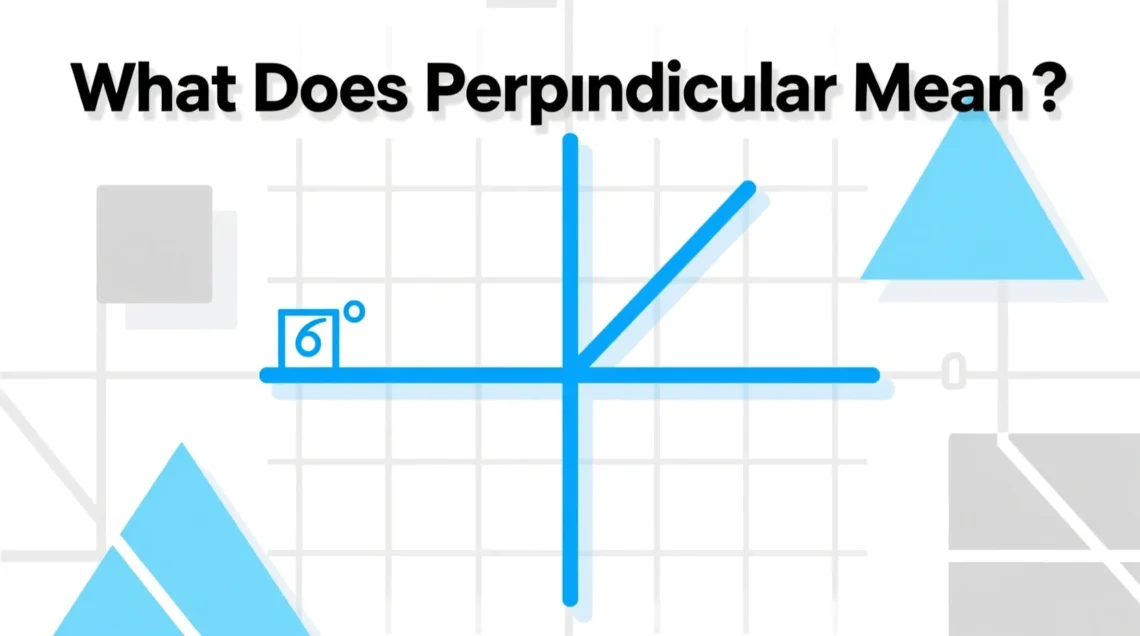
Geometry may sound intimidating, but some of its most important ideas are simple — and incredibly useful. One of those is the concept of perpendicular lines. Whether you’re designing a building, drawing a map, or simply looking at a street intersection, you’re surrounded by perpendicular structures.
This guide breaks down what “perpendicular” means, explains how it works in geometry and real life, and gives you examples, diagrams, and explanations that make this mathematical term easy to remember and apply.
Perpendicular Meaning: The Core Definition
The term “perpendicular” describes two lines, segments, or planes that meet at a right angle — that’s an angle of exactly 90 degrees.
If two lines form a square corner where they meet, they are perpendicular.
Word Origin
The word perpendicular comes from the Latin word perpendiculum, meaning “a plumb line” — a tool used to measure exact vertical alignment. Over time, it evolved to describe anything forming a straight, upright, or right-angled position.
Grammatical Forms
- Adjective: “The wall is perpendicular to the floor.”
- Noun: “The perpendicular marks the vertical direction.”
So, the next time you see two surfaces meeting cleanly at a right angle, you can say they’re perpendicular — just like the corners of a room.
Understanding the Perpendicular Angle (90°)
At the heart of perpendicularity lies the right angle — an exact 90-degree angle. It’s the cornerstone of geometry, architecture, and even computer graphics.
┌─┐ │ │ ← 90° └─┘
This shape is more than just a corner — it’s a perfect balance between two directions.
Comparing Angles
| Type of Angle | Measurement | Description | Example |
|---|---|---|---|
| Acute | Less than 90° | Sharp, narrow angle | A slice of pizza |
| Right | Exactly 90° | Perfect square corner | Book edge |
| Obtuse | More than 90° | Wide angle | Open door |
Perpendicular in Geometry
In geometry, perpendicularity describes the precise relationship between lines, planes, and shapes.
Two lines, segments, or planes are perpendicular if they intersect at a right angle (90°).
Perpendicular Lines
Two straight lines that cross each other at 90°. Example: the x-axis and y-axis on a graph. Symbol: AB ⊥ CD means line AB is perpendicular to line CD.
Perpendicular Planes
Two flat surfaces that intersect at a right angle. Example: the wall of a room (vertical plane) and the floor (horizontal plane).
Perpendicular Bisector
A line that cuts another line exactly in half and forms a right angle with it. Used in geometry problems, construction, and coordinate geometry proofs.
How to Identify Perpendicular Lines
In Geometry (Visual Identification)
- Look for the small square symbol (∟) marking a right angle.
- Check if they form the shape of a perfect corner.
- Use a protractor — the angle should measure exactly 90°.
In Coordinate Geometry (Mathematical Rule)
Two lines are perpendicular if the product of their slopes equals –1.
If Line 1 has a slope of m₁ and Line 2 has a slope of m₂, then:
m₁ × m₂ = -1
Example
Line 1 slope = 2
Then Line 2 (perpendicular to it) must have a slope of:
m₂ = -1/2
Real-Life Examples of Perpendicular Lines
Perpendicular lines aren’t just in textbooks — they’re everywhere you look.
| Example | Where You See It | Why It’s Perpendicular |
|---|---|---|
| Street intersections | Crossroads, traffic grids | Roads cross at right angles |
| Buildings | Wall and floor | Creates stability |
| Flagpoles | Flagpole and ground | Stands vertically upright |
| Television or phone screens | Screen edges | All corners are 90° |
| Graph paper | Grid lines | Perfect perpendicular network |
Fun Fact: City planners use perpendicular intersections to design grid-based street layouts. That’s why Manhattan looks like a checkerboard — efficient, organized, and perfectly perpendicular.
Perpendicular vs Parallel: What’s the Difference?
| Feature | Perpendicular | Parallel |
|---|---|---|
| Intersection | Yes — at 90° | No — never meet |
| Symbol | ⊥ | ∥ |
| Angle Formed | Right angle (90°) | No angle |
| Example | Wall and floor | Train tracks |
Applications of Perpendicular in Math and the Real World
In Geometry
- Rectangles, squares, and right triangles all rely on perpendicular lines.
- Coordinate axes (x and y) are perpendicular, forming the grid for graphing.
- Construction of bisectors, heights, and midpoints depends on perpendicularity.
In Trigonometry
The sine, cosine, and tangent ratios in right triangles are based on perpendicular relationships.
In Architecture and Engineering
Builders rely on perpendicularity to ensure buildings are safe, upright, and level. Surveyors use perpendicular distances to map land accurately.
In Computer Graphics and Design
- 3D modeling software uses perpendicular (orthogonal) axes — x, y, z — to define space.
- Perpendicular vectors help set object orientations and camera angles.
Perpendicular in Coordinate Geometry
Slope Relationship
If one line has a slope m₁ and another line is perpendicular to it, then:
m₂ = -1/m₁
Worked Example
Line 1 equation: y = 2x + 3
Then Line 2 must have slope -1/2 to be perpendicular.
The Perpendicular Distance Formula
To find the shortest distance from a point to a line:
Distance = |Ax + By + C| / √(A² + B²)
Example
Find the perpendicular distance from (2, 3) to the line 3x + 4y - 10 = 0:
|3(2) + 4(3) - 10| / √(3² + 4²) = 8/5 = 1.6
The point is 1.6 units away from the line.
Related Geometric Terms and Vocabulary
| Term | Meaning | Example |
|---|---|---|
| Right Angle | 90° angle formed by perpendicular lines | Corner of a square |
| Intersecting Lines | Lines that cross each other at any angle | Letter “X” |
| Orthogonal | Another word for perpendicular | Orthogonal vectors |
| Vertical Line | Line going straight up and down | y-axis |
| Horizontal Line | Line running left to right | x-axis |
How to Draw and Verify Perpendicular Lines
Drawing by Hand
- Use a ruler and set square to align and draw accurate perpendiculars.
- Use graph paper for built-in perpendicular guides.
- Check the corner with a book edge or right-angle tool.
Using a Compass and Straightedge
- Draw a line segment (AB).
- Place the compass on A and draw an arc crossing the line twice.
- Repeat from each crossing point to form an “X” above the line.
- Draw a line through A and the intersection of arcs — that’s the perpendicular.
Fun Facts About Perpendicular Lines
- Skyscrapers: Engineers use lasers to ensure buildings stay perfectly perpendicular to the ground.
- Ancient Egyptians: Used plumb bobs to align pyramid edges — early perpendicular tools.
- Computer Monitors: Display pixels in perpendicular rows and columns for clarity.
- Navigation Systems: Use perpendicular reference axes to calculate direction.
The Role of Perpendicularity in Shapes
| Shape | Perpendicular Lines | Description |
|---|---|---|
| Square | 4 pairs | All sides meet at 90° |
| Rectangle | 4 pairs | Opposite sides parallel, corners perpendicular |
| Right Triangle | 1 pair | Legs form a 90° angle |
Common Mistakes About Perpendicular Lines
- All perpendicular lines intersect, but not all intersecting lines are perpendicular.
- Perpendicular slopes are negative reciprocals — not just opposite numbers.
- Parallel lines never meet; perpendicular lines always meet once at 90°.
- Always include units when calculating perpendicular distance.
Perpendicular in Physics and Engineering
In Physics
- Force and Motion: Perpendicular forces determine balance and direction.
- Magnetic Fields: Field lines are perpendicular to electric current.
- Light Reflection: Normal lines are perpendicular to surfaces.
In Engineering
- Bridges and towers use perpendicular beams for stability.
- Blueprints depend on perpendicular reference lines for accuracy.
The Symbol for Perpendicular (⊥)
In mathematics, the symbol ⊥ represents “is perpendicular to.”
AB ⊥ CD: Line AB is perpendicular to line CD.x ⊥ y: x-axis is perpendicular to y-axis.
FAQs About Perpendicular Lines
Q1. What does perpendicular mean in geometry?
It means two lines or planes meet at a 90° angle.
Q2. Are perpendicular lines always straight?
Yes — they’re straight lines that cross at right angles.
Q3. Can two planes be perpendicular?
Absolutely. The floor and wall of a room are perfect examples.
Q4. What’s the perpendicular symbol?
It’s the ⊥ symbol.
Q5. What’s perpendicular distance?
It’s the shortest distance from a point to a line, measured at a right angle.
Q6. How do you check if two lines are perpendicular?
By ensuring their slopes multiply to –1 or by confirming they meet at a 90° angle.
Summary: Why “Perpendicular” Matters Everywhere
Perpendicular lines shape both our mathematical understanding and our physical world. From the corners of buildings to the coordinate axes of graphs, they form the foundation of structure, stability, and order.
Here’s what you’ve learned:
- Definition: Two lines or planes meeting at 90° are perpendicular.
- Symbol: ⊥
- Core Use: Geometry, trigonometry, architecture, and design.
- Real-world presence: Everywhere — roads, walls, furniture, screens, and more.
Perpendicularity isn’t just geometry — it’s the silent rule that keeps the world balanced, upright, and perfectly aligned.
Quick Reference Table
| Concept | Definition / Formula | Example |
|---|---|---|
| Perpendicular Lines | Intersect at 90° | Floor and wall |
| Slope Rule | m₁ × m₂ = -1 | 2 × -½ = -1 |
| Perpendicular Symbol | ⊥ | AB ⊥ CD |
| Perpendicular Distance | |Ax + By + C| / √(A² + B²) | 1.6 units |